This entry describes the mathematical derivation of the Maastricht criteria (hereinafter: Mc) ratios and it reveals that the initial economic assumptions - which were the basis for the ratio calculations - were completely wrong and uncertain.
In the following only elementary, secondary school level mathematics is used and thus is tractable with an equivalent degree. Alternatively, it can be omitted if one does not desire to follow through the derivations.

The mathematical derivation of the Mc targets shows that the 3% deficit ratio criterion was based on the following three wrong or insecure assumptions:
- GDP grows with a rate of 5% (2% inflation + 3% growth).
- Only the 60% public debt / GDP ratio (public debt ratio) is able to ensure economic convergence and price stability in the Member States.
- MC focuses solely on the relationship between credit money (with other words, fiat money) creation by public debt and GDP (we will see in this paper later that the amount of fiat money = the amount of debt) and does not take into account the role of the financial intermediary system in creating money (= debt) and supporting the GDP.
Without the above mentioned 3 assumptions, the Maastricht criteria do not make any sense whatsoever. However, these 3 assumptions are wrong and unrealistic.
Note: the formula below expresses the usual assumption that the annual growth of public debt is the same as the annual deficit (or: previous year's public debt + this year's deficit = public debt in this year).
D (t) = public debt at (t) year
D (t-1) = Public debt (t-1) year
d = deficit
D (t) -D (t-1) = d (t)
Divide this equation with GDP generated in period (t), denoted by GDP (t). We get this:
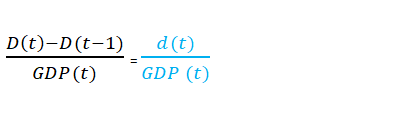
Notice that the right-hand side is the deficit rate.
We divide the numerator and denominator of the second member of the term on the left-hand side with by the GDP of the previous year, GDP (t-1). We get the following relationship:
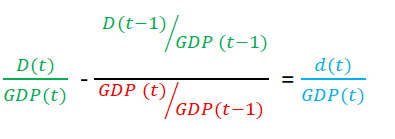
If the debt ratio, which is denoted by Dr(t), is unchanged, ie
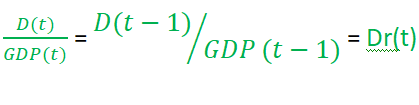
then the above relationship can be written in the form below
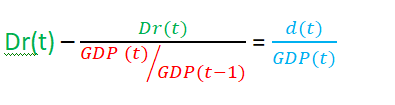
Let's call 1 + g(t) the GDP growth rate in t-period:
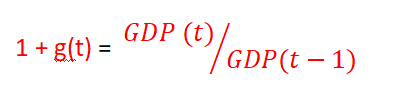
and write the above formula again:
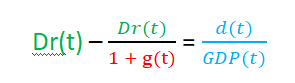
multiply both sides by 1+g(t)
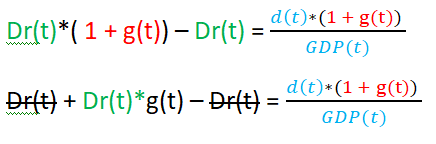
Divide both sides by 1+ g(t)
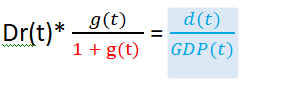
This is the deficit rate.
Thus, if we assume a 5% increase and we aim to maintain a maximum debt ratio of 60%, we get a 3% deficit rate based on the above formula.
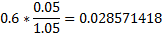
which is rounded to a 3% deficit rate.
Thus, the 3% deficit ratio follows from keeping the 60% government debt as a target value, assuming a 5% GDP growth rate.
Why 60 % is the target number of public debt/GDP?
Why only the maximum 60% government debt rate is capable of ensuring financial stability? Why a higher level of debt cannot be tolerated if growth slows down and the willingness to accumulate money (or securities) is increasing? Neither the Delors Committee nor the economic experts (community of economists) have provided an exact explanation, especially not when the shock or GDP decline was triggered by the disruptions of the financial intermediary system itself, as in September 2008.
According to the literature, only these rigid regulations could convince the Germans and the northern states that the southern states would be included in the monetary union. (McKinnon, 1997, Buti and Sapir 1998). This is based on political considerations and thus cannot be respected to be an economic argument.
The self-critical approach of the above-mentioned regulatory hypothesis at the level of the IMF already emerged in 2012, when IMF Chief Economist Olivier Blanchard admitted that
"We assumed we could ignore the details of the financial system."
What is the stability of finance?
The purpose of the Maastricht Criteria, at least in principle is to provide 'financial stability' to the States who subscribe to its principles.
According to the European Central Bank’s definition: “Financial stability can be defined as a condition in which the financial system – intermediaries, markets and market infrastructures – can withstand shocks without major disruption in financial intermediation and in the effective allocation of savings to productive investment.”
Instability: starting from the ECB’s above-mentioned definition, the financial system may become unstable if banks fail to finance each other, resulting in the stalling of the allocation of resources.
In this case, the value of the loan collateral assets (eg. bonds, real estate, etc.) begins to decrease (stress situation), therefore the improvement of the capital adequacy ratios (balance sheet adjustment) requires credit constraint or additional funding. (This, of course, also reduces the resources available in the real sector, so the L/V ratios (loan to asset value) may further deteriorate through the narrowing of the demand market.)
Stability: financial stability is, of course, based on a climate of trust and stable solvency of the debtors of the banks, which would require a relatively stable demand market.
The hidden philosophy of the Maastricht criteria system:
The monetary-based work hypothesis, which has been associated with the neoliberal philosophy can be summarized in the following;
the money entering the economic circle through government measures (or non-spontaneous, market-based mechanisms), can only lead to inflation in the long run.
Therefore, at the beginning of the 1990s, regulators tried to limit the possibility of state intervention, and they were confident that price stability would automatically lead to financial stability.
The issue of price stability was also promoted with the requirements of public finances based on the target numbers.
Please note, that this logic completely ignores the role of the banking system's credit activity in creating money! It solely focuses on keeping an average of 60% of government
debt / GDP,
which was only a periodical ratio at the early 1990s. It reveals that the creators of the criteria modeled the economy based on the assumption that the only player influencing the amount of money in the system is the State itself!
Painful consequences:
Unfortunately, the financial market could collapse triggered solely by the market itself. However, in this case, the Maastricht legislation does not provide governments with the discretion to intervene: they have an obligation to watch idly the destruction and keep on maintaining the fiscal balance even during the period of an economic collapse.
Since 2010, financial stability has been threatened by the possibility of government bankruptcy itself, as the directives of the Stability and Growth Pact hinder central banks and countries from propping up their own budgets and those of their partner countries.
The governments have no effective means in the form of fiscal instruments when the markets start to collapse.
The role of the financial system in the evolution of the money quantity (money creation):
The basis of the credit money system is the recording of the amount of the official currency (legal tender), i.e. the accounting where every "source entry" on the DEBIT side has to have an attached "claim entry" on the other side of the balance sheet, in the CREDIT (asset) side.
There is no money in the system as a whole, without its debt counterpart.
Since the legal tender (coins) can only be created by the state (private money printing is counterfeit), we can imagine as a first step in creating money, that the central bank issues cash (or loan money) for some economic purpose, either to the state (government) or to the commercial banks. Thus, the central bank's balance sheet receivables (assets) include a claim from the state or the bank. The cash is the obligation of the central bank (in accounting terms) at the same time. Just take a look at the phrase on any banknote in England!
"I promise to pay the bearer on demand the sum of five pounds"
Once again: the cash and coins are essentially the central bank's debt, so the paper money or coin is the state's promise of payment (a more civilized version of an "I owe you"), i.e. public debt.
When a government pays 100 units of money for a service to its provider, who, as a depositor, places this 100 units of money at his bank, then his bank has the ability to lend 80 units, because 20 units are the reserve obligation. (Say r = 20%).
The bank's new debtor spends these 80 units at somebody's shop, so his seller’s bank can continue to lend 80% (64 units) of the money deposited by the seller (80), and so on. The process is a geometric sequence where the quotient (q) is 0.8. The sum of the members of the infinite geometric line
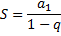
where a(1) = 100 units.
Therefore, the banking system can generate a total of 500 units of money, with 500 cash claims and 500 unit debts. "1 / t" is called money multiplier.
Thus, the banking system has 1 unit of central bank money, “external money” or money created by public debt, and it can make it 5 times more (given a reserve ratio of 0,2). We re-emphasize the accounting fact that each money unit is a debt unit of someone else (if the debtor is the government, then public debt, if a private-owned bank, then private debt).
The cessation of money unit:
When a net creditor buys something from a net debtor and the debtor pays off his debt from this fresh income, the creditor's claim for money and the debtor's debt is reduced, so the money units are deleted from the accounting system.
As the amount of money (= debt stock) can be reduced if the net creditor buys something from the net debtors, the stock of external debt or international debt (the stock of foreign exchange reserves, in short: national reserves) can be reduced. This will happen if the regions which have accumulated trade and balance of payments surpluses in the previous period, start to consume (or confiscate) the products and assets of regions that accumulate passives in the past.
In the opposite direction: if we have increasing national reserves, it means there is an increasing foreign debt somewhere else.
When the time of perfect trade balance will come, there will be no need for money units. No debt, no reserves, no money.
GDP
We have drawn attention to the importance of the equivalence of the two accounting sides of money (Amount of money = amount of debt), we do this again in the case of GDP:
there is no production without consumption, ie no income can be generated without spending money.
(In the case of “inventory”, when there is a pile of unsold goods in the stock, it is taken into account as the producer's income and the same producer’s expenditure).
For the global world economy Gross Domestic Product (Gross “Global” Product) =
GDP = annual consumption = annual output = annual expenditure = annual income.
Equivalences, Conclusions:
The "debt / annual income" indicators (for example: debt/GDP) are equivalent to the "savings / annual consumption" indicators. If there is a growing tendency for savings in a closed system of the globalized world economy, it will increase
the 'savings / annual consumption' ratio,
which obviously means that 'debt / annual income', (for example "debt / GDP" ratio) must increase', and it might be good news.
If you want to take care of your own future, you probably accumulate more and more money as savings. If it is great merit, a sign of financial literacy, and as a top of it all, an actual process in global scale, then the increase of the "savings / annual consumption" ratio, which equivalent with the "debt / GDP" ratio, so this debt percentage increase cannot be a source of problems.
The conclusion is that an increase of savings in cash or government securities might mean the growth of the "public debt / GDP", so the increase of this ratio alone cannot be an economically harmful, dangerous trend, rather a natural phenomenon.
More questions about the sense of fixing a 60% government debt rate:
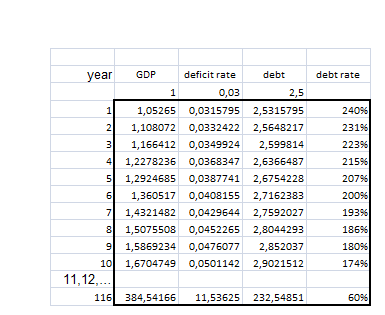
Based on Maastricht logic presented above, the following deficit ratios fall under the different debt ratios and different nominal GDP growth rates. The horizontal values in the header contain the nominal rate of growth. The first vertical column of the sidebar is the government debt per GDP rate. The internal numbers of the table are the deficit/GDP ratios at which the given debt ratio can be maintained along with the GDP growth - at least, according to the Maastricht formula.
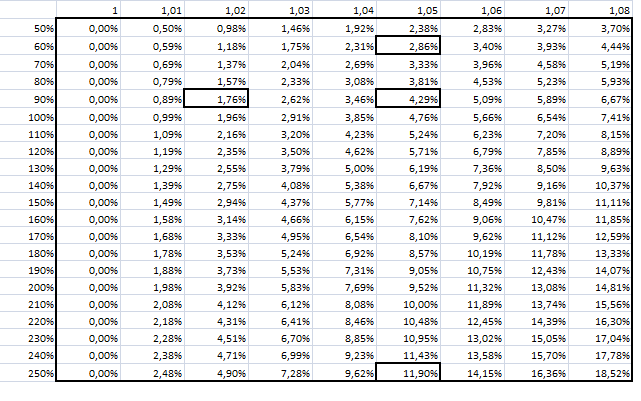
Let us take the example of a developed country’s economy, for instance, that of Japan‘s, and inspect it in the Mc’s framework. We will quickly find out that Japan's public debt / GDP is approx. 250%. Hence, if Japan were able to achieve a GDP growth of around 5% (real and inflation growth of around 2 -3%), keeping its debt level would become possible, even with an 11.9% deficit/GDP ratio.
When will Japan be matured enough to deserve the euro?
If Japan produced a nominal growth rate of 5.26% a year with a 3% annual government deficit ratio, it would reach the 60% government debt ratio in 116 years, the euro maturity according to the MC. It seems a long time...
What could be the deficit rate if the EU were to stand on a 5% growth path now?
The economic history of the eurozone has resulted in the economy of approx. 90% -95% debt-to-GDP ratio by 2015. If the economy started to return to a stable 5% growth path (with real growth of about 2 -2.5% and inflation between 2-2.5%) then keeping the debt ratio of 95% would mean that the tolerable current deficit could be raised to 4.5%.
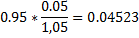
However, if the growth is nominally approx. 2% (in which real growth is about 1% and inflation is 1%), the deficit ratio should be tightened from the current 3% to 2% in order to keep the 90% government debt rate, otherwise, it is prone to climb up ...
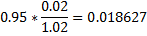
We are not aware of any evidence that would justify fixing a rate ideal for economic stability. Choosing any destination is arbitrary. If the deficit rate is fixed, the debt ratio will change depending on the growth rate.
The importance of private debt as a form of savings:
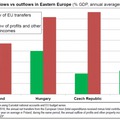
The one who collects money may also decide not to keep her/his money in government securities or in cash but in bank deposits or in other financial instruments. In this case, private debt appears behind the money - provided that the banks are privately owned. Account money is the passivity (debt) of the banking system. The data below show that a growing proportion of money is not made up of government or public debt but private debt. In the case of the countries signing the MC, "private debt / GDP" is more than 350%.
This implicitly means that public debt (state spending) has less and less influence on the price level. The evolution of GDP, money and price levels increasingly depends on the behavior and opportunities of the private sector affected by bank credit activity/passivity.
Mc signatories debt ratios
- Signatories: Belgium, Denmark, Germany, Ireland, Greece, Spain, France, Italy, Luxembourg, Netherlands, Portugal, United Kingdom.
- Data: Since 1995, without Ireland and Luxembourg. The table below shows the proportions of the ten countries:
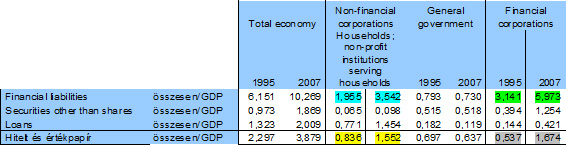
The data show that the total corporate and household debt increased from around 200% to 350% of GDP between 1995 and 2007. Within this, credit-type debt (securities and loans) rose from 84% to 155%, ie almost doubled in volume. (Meanwhile, the public debt ratio has fallen!)
All this was due to the strong activity of the financial sector, as shown by the fact that its total liabilities increased from 3 times in 1995 to 6 times of the GDP in 2007.
The above processes underestimate the actual process because the financial activity of the two missed countries is the most powerful (since we have data). Moreover, in the former socialist countries, there was hardly any lending before the change of regime (Hungary was the most advanced in this field), so the rise of credit-based financing was much higher than in the above-mentioned countries, ie it also rose rapidly (from level zero a small increase results in infinite growth.)
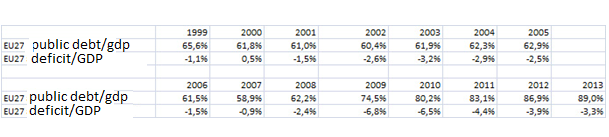
Meanwhile, by 2007, aggregate fiscal ratios of the EU countries, which we use for examining the healthiness of an economy, did not point to any problems that could jeopardize financial stability:
Call for reforms
The situation is further exacerbated by the laws which prohibit the central banks ( including the European Central Bank) from direct financing of public debts and ban member states from bailing each other out (this is called: ”no-bailout clause”).
The lack of a scientifically sustainable justification can be a serious threat to the future of the European Union, since the EU system of legal and financial sanctions is currently based on, without any reason, a budget balance approach defined by the 3% deficit limit. This results in insufficient financing in a number of vital areas such as environment and healthcare, and, when the economy driven by private forces sails through troubled waters, the governments must turn against their own people instead of stimulating transactions or helping the victims.
Between 16 February and 23 March 2015 together with László Náray (former vice president of the Hungarian Financial Supervisory Authority) in the “Standpoint” section of the newspaper called “Daily Economy” in Hungary we argued in a series of five articles that the imposition of the Maastricht criteria was anachronistic and presents a threat to the existence of the European Union.
We have therefore initiated a substantive debate based on economic arguments
- the reason for the Maastricht Criteria system,
- its role in the financial crisis that began in 2008
- and its effectiveness as a crisis management tool.